Real Analysis

微分（MIRA）

本篇核心内容梗概

首先介绍Hardy-Littlewood极大不等式，不过，为此需介绍一些前置的概念，包括$\mathcal{L}^1(\mathbb{R})$相关的内容。其中，定理（连续函数逼近$\mathcal{L}^1(\mu)$成员）的证明又需要阶梯函数相关的很多结论，为不影响主线，暂略

在Hardy-Littlewood极大不等式以及（曾经接触过的）Markov不等式的帮助下，得到Lebesgue微分定理。Lebesgue微分定理，可以粗略当成微积分基本定理（形式之一）的替代版本

前置概念

定义 （$\mathcal{L}^1(\mu)$与$\Vert f\Vert_1$）

• 测度空间$(X,\mathcal{S},\mu)$，$f:X\to[-\infty,\infty]$是一个$\mathcal{S}$可测的函数，那么，$f$的$\mathcal{L}^1$范数定义为$\Vert f\Vert_1 = \int \vert f\vert d\mu$ 。

• Lebesgue空间$\mathcal{L}^1(\mu)$，被定义为$\set{f\text{ from }X \text{ to } \mathbb{R} : f\text{ is }\mathcal{S}\text{ measurable function s.t.} \Vert f\Vert_1 < \infty}$

$\mathcal{L}^1(\mu)$的具体例子：当$X$取成$\mathbb{Z^+}$，$\mu$取计数测度时，就演化为绝对收敛的实数序列的集合，即满足$\sum\limits_{k=1}^\infty \vert x_k\vert<\infty$的序列

此外，这个$\Vert f\Vert_1$显然几条性质：

• $\Vert f\Vert_1 \geq 0$；

• $\Vert f\Vert_1 = 0$当且仅当几乎处处$f(x) = 0$：右推左显然，左推右用定理（递增集合的测度极限）

• $\Vert c f\Vert_1 = \vert c\vert \Vert f\Vert_1$对$\forall c\in\mathbb{R}$成立

• $\Vert f+g \Vert_1\leq \Vert f \Vert_1+\Vert g\Vert_1$

定理 （连续函数逼近$\mathcal{L}^1(\mu)$成员）
若$f\in \mathcal{L}^1(\mathbb{R})$，则对任意$\varepsilon>0$，均存在一个连续函数$g:\mathbb{R}\to \mathbb{R}$使得：$\Vert f-g\Vert_1< \varepsilon$，并且$\set{x\in \mathbb{R}:g(x)\neq 0}$是有界子集

证明：略，见书本3.48

Hardy-Littlewood极大不等式

定理 （Markov不等式）
测度空间$(X,\mathcal{S},\mu)$中，$h\in \mathcal{L}^1(\mu)$，则对$\forall c>0$有：
$$
\mu( \set{x\in X:\vert h(x)\vert\geq c})\leq \frac{1}{c}\Vert h\Vert_1
$$

该不等式，在学概率论时就接触过，证明很简单（《概率导论》中还有该证明的直观示意图）：

$$
\begin{align*}
& \mu( \set{x\in X:\vert h(x)\vert\geq c}) = \frac{1}{c}\int_{\set{x\in X :\vert h(x)\vert\geq c}} cd\mu \\
\leq & \frac{1}{c}\int_{\set{x\in X :\vert h(x)\vert\geq c}} \vert h\vert d\mu \leq \frac{1}{c}\int_X \vert h\vert d\mu \\
\end{align*}
$$

$\square$

定义 （3倍区间记号）
$I$是一个$\mathbb{R}$上的、有界的、开区间，则$3 * I$这个记号代表中心和$I$一样的，但是长度为$I$的三倍的那个区间（画个图很直观）

下面这个引理，是个有趣的小结论（初次见到时还挺意外的）：

定理 （Vitali覆盖引理）
$I_1,I_2,\dots I_n$是$\mathbb{R}$上的有界非空开区间，那么，可以取其中互相无交的一部分$I_{k_1},I_{k_2},\dots I_{k_m}$，使得$\bigcup\limits_{j=1}^m 3 * I_{k_j} \supset \bigcup\limits_{j=1}^n I_n$

证明：核心是给出一个找$I_{k_j}$的算法，并证明能达到效果。这里的算法就是贪心算法！和图论中的“最小生成树”（MST）的构造异曲同工

算法陈述：先把$I_1,\dots I_n$按照长度由大到小重新排列，然后将这个新序列逐个弹出：若弹出的新成员与先前“采纳”的成员无交，那么“采纳”这个新成员；else，舍弃。然后弹出下一个……直到遍历完成

验证算法正确，只需任取$i$，证明$I_i\subset\bigcup\limits_{j=1}^m 3 * I_{k_j}$：若$I_i$本身在算法执行过程中就被“采纳”了，那显然正确；若$I_i$未被“采纳”，说明它和之前已经“采纳”的成员（记为$I_{k_l}$）有交集，但$I_{k_l}$长度一定更大，所以$3 * I_{k_l}\supset I_i$成立

$\square$

现在，可以开始讨论Hardy与Littelwood的工作了！

定义 （Hardy-Littlewood极大函数）
设$h:\mathbb{R}\to\mathbb{R}$是Lebesgue可测的，则定义$h$的Hardy-Littlewood极大函数$h^\ast: \mathbb{R}\to [0,\infty]$为：
$$
h^\ast (b) = \sup_{t>0} \frac{1}{2t}\int_{b-t}^{b+t} \vert h\vert
$$

助于理解的直观例子：

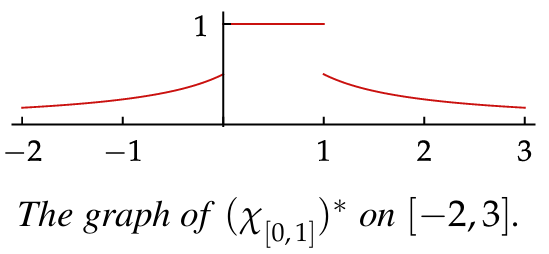
定理 （$h^\ast$Borel可测）
若$h:\mathbb{R}\to \mathbb{R}$是一个Lebesgue可测的函数，则可如上定义其Hardy-Littlewood极大函数$h^\ast: \mathbb{R}\to [0,\infty]$，且该函数是Borel可测的

证明：下面证明“$\set{b\in \mathbb{R}: h^\ast(b)>c}$是个开集”，因为根据定理（可测函数的等价条件），此命题得证后原命题得证

只需证明：任取$b_0\in \set{b\in \mathbb{R}: h^\ast(b)>c}$，$b_0$都是内点

根据定义，$\exists L,\varepsilon>0$使得$\frac{1}{2L}\int _{b_0-L}^{b_0+L} \vert h\vert >(1+\varepsilon) c$，因此，可取任意$b’\in (b_0-\varepsilon L ,b_0+\varepsilon L)$，发现$b’$也是$\set{b\in \mathbb{R}: h^\ast(b)>c}$中的点，因为$\frac{1}{2(1+\varepsilon L)}\int _ {b’ - (1+\varepsilon L)} ^{b’+(1+\varepsilon L)}\vert h\vert > \frac{1}{2(1+\varepsilon L)}\int _ {b_0-L}^{b_0+L}\vert h\vert >c$

因此$b_0$是内点

$\square$

定理 （Hardy-Littlewood极大不等式）
设$h\in\mathcal{L}^1(\mathbb{R})$，则对于任意的$c>0$，均有：
$$
\vert \set{ b\in\mathbb{R}: h^\ast(b) >c}\vert \leq \frac{3}{c}\Vert h\Vert_1
$$

证明：由于$\set{ b\in\mathbb{R}: h^\ast(b) >c}$是一个Borel集（根据上一个定理），所以，由定理（Lebesgue可测集的等价定义），必定能找到里头的一个闭集$F$，和该集合“大小接近”。因此，欲证原命题，只需证：“任何有界闭集$F\subset \set{ b\in\mathbb{R}: h^\ast(b) >c}$，均有$\vert F\vert \leq \frac{3}{c}\Vert h\Vert_1$”

根据定义，$\forall b\in F$均存在$t_b$使得：$\frac{1}{2t_b}\int _ {b-t_b} ^{b+t_b} \vert h \vert>c$

由于$F\subset \bigcup\limits_{b\in F}(b-t_b,b+t_b)$平凡地成立，自然得到一个开覆盖，大名鼎鼎Heine-Borel助威，得到有限子覆盖：$F\subset (b_1-t_{b_1},b_1+t_{b_1})\cup(b_2-t_{b_2},b_2+t_{b_2})\dots\cup (b_n-t_{b_n},b_n+t_{b_n})$，为了简洁，右侧干脆记为$I_1\cup\dots I_n$

现在，根据Vitali覆盖引理，选出其中部分无交成员$I _ {k _ 1},I _ {k _ 2}\dots,I _ {k _ m}$，满足其3倍区间之并覆盖原来的区间并

$$
\begin{align*}
& \vert F\vert \leq \vert I _ 1\cup I _ 2\cup\dots \cup I _ n\vert\leq \vert 3 \ast I _ {k _ 1}\cup 3 \ast I _ {k _ 2}\cup\dots\cup 3 \ast I _ {k _ m} \vert \\
\leq & \vert 3 \ast I _ {k _ 1} \vert +\vert 3* I _ {k _ 2}\vert \dots \vert 3 \ast I _ {k _ m} \vert = 3(\vert I _ {k _ 1} \vert +\vert I _ {k _ 2}\vert \dots \vert I _ {k _ m} \vert) \\
< & \frac{3}{c} \left(\int _ {I _ {k _ 1}} \vert h\vert + \int _ {I _ { k _ 2}} \vert h\vert + \dots +\int _ {I _ {k _ m}} \vert h\vert \right)\leq \frac{3}{c} \int \vert h\vert \\
\end{align*}
$$

Lebesgue微分定理

定理 （Lebesgue微分定理 ver.1）
若$f\in \mathcal{L}^1(\mathbb{R})$，则下式对几乎处处$b\in \mathbb{R}$成立：
$$
\lim_{t \downarrow 0} \frac{1}{2t}\int_{b-t}^{b+t} \vert f-f(b)\vert = 0
$$

证明：调用定理（连续函数逼近$\mathcal{L}^1(\mu)$成员），对于固定的$k\in \mathbb{Z^+}$都能找到连续函数$h_k$满足：$\Vert f-h_k\Vert_1 < \frac{\delta}{k 2^k}$，构造$B_k = \set{b\in \mathbb{R}: \vert f(b)-h_k(b)\vert\leq \frac{1}{k} \text{ and } (f-h_k)^\ast(b)\leq \frac{1}{k}}$。因此，$f$与$h_k$“有较大分歧”的集合就是其补，$\mathbb{R}-B_k$

由于$\mathbb{R}-B_k=\set{b\in \mathbb{R}: \vert f(b)-h_k(b)\vert> \frac{1}{k} }\cup \set{b\in \mathbb{R}:(f-h_k)^\ast(b)>\frac{1}{k}}$，我们欲知，该集合“多大”呢？正好，可以用Markov不等式解决第一部分，Hardy-Littlewood极大不等式解决第二部分！

Markov不等式导出$\vert \set{b\in \mathbb{R}: \vert f(b)-h_k(b)\vert> \frac{1}{k} }\vert <\frac{\delta}{2^k}$，Hardy-Littlewood极大不等式导出$\vert \set{b\in \mathbb{R}:(f-h_k)^\ast(b)>\frac{1}{k}} \vert < \frac{3\delta}{2^k}$，因此，$\mathbb{R}-B_k$集合很小：$\vert\mathbb{R}-B_k \vert<\frac{\delta}{2^{k-2}}$

现在，令$B =\bigcap\limits_{k=1}^\infty B_k$，根据上一段，有$\vert \mathbb{R} - B\vert<4\delta$。这个$B$就是要找的“处处成立”的那个集合！

下面，我们来看，为什么在$B$上命题严格成立

若$b\in B,t>0$则对于任何$k\in \mathbb{Z^+}$，使用中间人把戏：

$$
\begin{align*}
& \frac{1}{2t}\int_{b-t}^{b+t} \vert f-f(b)\vert \leq \frac{1}{2t}\int_{b-t}^{b+t} (\vert f-h_k\vert +\vert h_k - h_k(b)\vert +\vert h_k(b) -f(b)\vert) \\
\leq & (f-h_k)^\ast (b) + \frac{1}{2t}\int_{b-t}^{b+t} \vert h_k-h_k(b)\vert + \vert h_k(b) -f(b)\vert \\
\end{align*}
$$

观察首项和末项，根据$B_k$的定义，它们都被$\frac{1}{k}$压制，因此上式$\leq \frac{2}{k} + \frac{1}{2t}\int_{b-t}^{b+t} \vert h_k-h_k(b)\vert$

简单放缩剩余的一项：$\frac{1}{2t}\int_{b-t}^{b+t} \vert h_k-h_k(b)\vert \leq \sup \set{\vert h_k(x)-h_k(b)\vert: x\in [b-t,b+t]}$，别忘了$h_k$是连续的，因此，随$t$减小，右侧可任意小

因此，整个式子都被镇压住了，结论是：$\lim\limits_{t\downarrow 0 }\frac{1}{2t}\int_{b-t}^{b+t} \vert f-f(b)\vert \leq \frac{3}{k}$，因此在$B$上，即$\lim\limits_{t\downarrow 0 }\frac{1}{2t}\int_{b-t}^{b+t} \vert f-f(b)\vert =0$

$\square$

定理 （Lebesgue微分定理 ver.2）
若$f\in \mathcal{L}^1(\mathbb{R})$，则定义$g:\mathbb{R}\to \mathbb{R}$如下
$$
g(x) = \int_{-\infty}^x f
$$
则，$g’(b) = f(b)$在$b\in \mathbb{R}$几乎处处成立

证明：若$t>0$，则如下（用了绝对值不等式）

$$
\begin{align*}
& \left\vert\frac{g(b+t)-g(b)}{t} - f(b)\right\vert = \left\vert\frac{ \int _ b ^{b+t} f -f(b)}{t}\right\vert \\
\leq & \frac{1}{t} \int _ {b}^{b+t} \vert f-f(b)\vert \leq \frac{1}{t}\int _ {b-t}^{b+t} \vert f-f(b)\vert \\
\end{align*}
$$

根据Lebesgue微分定理ver.1，可以发现随着$t \downarrow 0$等于0

若$t<0$同理，当$-t\downarrow 0 $时原式等于0，故得证