Real Analysis

Luzin的博士论文指导老师正是Egorov

可测函数收敛专题（MIRA）

本篇核心内容梗概

两个定理—Egorov定理和Luzin定理

Egorov定理

引入动机：早在数学分析课程中学习函数项级数时，我们就发现很多函数序列不是一致收敛的。但是，往往抠掉一个很小的区间，在剩下的集合上就能够一致收敛了，这不禁引人深思……也许，Egorov就是其中一位思考者

我们即将看到，Egorov定理其实就描述了这件事

定理 （Egorov）
设测度空间$(X,\mathcal{S},\mu)$，满足$\mu(X)<\infty$，而$f_1,f_2,\dots: X\to \mathbb{R}$是在其上定义的可测函数序列，且逐点收敛到$f:X\to \mathbb{R}$。那么，对于任何$\varepsilon>0$，均存在一个可测的集合$E$，使得$\mu(X-E)<\varepsilon$且该函数序列在$E$上一致收敛到函数$f$

证明：目标很清晰，就是给定$\varepsilon$后构造出$E$

对于固定的$n\in \mathbb{Z^+}$，都有如下式子成立（不过是复述逐点收敛的定义而已）

$\bigcup\limits_{m=1}^\infty \bigcap\limits_{k=m}^\infty \set{x\in X : \vert f_k(x) - f(x)\vert < \frac{1}{n} }=X$

因此，用双指标去记 $A_{m ,n} = \bigcap\limits_{k=m}^\infty \set{x\in X : \vert f_k(x) - f(x)\vert < \frac{1}{n} }$，那么$\bigcup\limits_{m=1}^\infty A_{m,n} = X$

此外，由于形成递增序列$A_{1,n}\subset A_{2,n}\subset \cdots$，再调用定理（递增集合的测度极限），可得$\lim\limits_{k\to\infty}\mu(A_{k,n}) = \mu(X)$，因此，存在一个$m_n$（必然和$n$有关，因为得先固定它）使得$\mu(X) - \mu(A_{m_n,n})<\frac{\varepsilon}{2^n}$，渐渐看出端倪了吧

令$E= \bigcap\limits_{n=1}^\infty A_{m_n,n}$，这就是所求！

验证测度大小（几何级数求和压制法）： $\mu(X-E)=\mu(\bigcup\limits_{n=1}^\infty (X-A_{m_n,n})) \leq \sum\limits_{n=1}^\infty \mu(X) - \mu(A_{m_n,n}) \leq \varepsilon$，的确如此

验证一致收敛：随便来一个$\delta >0$，都可找到$\frac{1}{n}<\delta$的那些$n$，而$E\subset A_{m_n,n}$，根据$A_{m_n,n}$的定义即知$\forall x\in E , \vert f_k-f \vert < \frac{1}{n}<\delta$对于$k>m_n$都成立

$\square$

可测差不多是简单的

定义 （简单函数）
仅仅取有限个值的函数就称为简单函数（simple function）

显然，简单函数可以写为$f=\sum\limits_{i=1}^m c_i \chi_{E_i}$。同样容易证明，$f$为可测函数当且仅当$E_1\dots E_m$均为可测集（将$E_i$写为$c_i$附近小区间的逆像即可）

定理 （用简单函数近似可测函数）
可测空间$(X,\mathcal{S})$上，函数$f:X\to[-\infty,\infty]$是一个可测函数（在广义实数系的Borel集意义下），那么，存在一个可测的简单函数序列$f_1,f_2\dots$，满足：

$\vert f_k(x)\vert \leq \vert f_{k+1}(x) \vert\leq \vert f(x) \vert \quad \forall k\in \mathbb{Z^+}, \forall x\in X$
$\lim\limits_{k\to\infty} f_k(x) = f(x)\quad \forall x\in X$
若$f$有界，则这个收敛是一致收敛

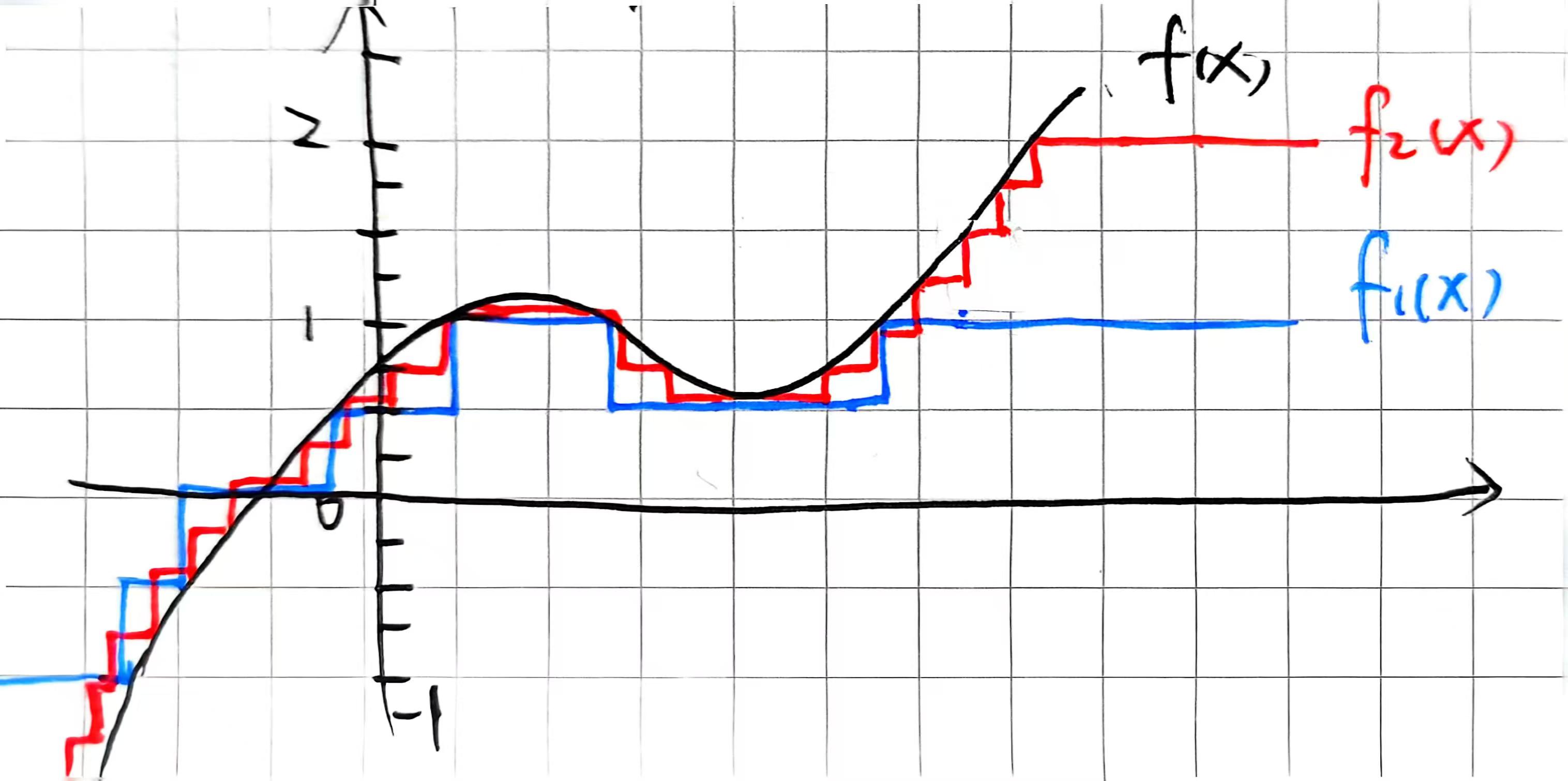
证明：看图就懂了，思路是把实轴分成$\frac{1}{2^k}$这么长的小段，然后构造的公式是这样：

$$
f_k(x) = \begin{cases}
\frac{m}{2^k} & 0\leq f(x) \leq k \quad f(x)\in[\frac{2}{2^k},\frac{m+1}{2^k}) \\
\frac{m+1}{2^k} & -k \leq f(x) < 0 \quad f(x)\in[\frac{2}{2^k},\frac{m+1}{2^k}) \\
k & f(x)>k\\
-k & f(x) < -k \\
\end{cases}
$$
显然这样的$f_k$是简单函数，而且由于$f$可测，因此$f^{-1}([\frac{m}{2^k}, \frac{m+1}{2^k}))$是可测集，因此简单函数写成可测集合特征函数的线性组合后，是可测的

这个收敛相关的结论也是容易的：$\vert f_k(x)-f(x)\vert\leq \frac{1}{2^k} \quad \forall x\in X \text{ s.t. }f(x)\in [-k,k]$

Luzin定理

Version 1

引入动机：之前已有定理（连续函数是Borel可测的），那么反之何如呢？Luzin定理回答了这个问题：反之，差不多也是对的

定理 （Luzin ver.1）
设$g:\mathbb{R}\to\mathbb{R}$是一个Borel可测的函数，那么对任意$\varepsilon>0$，存在一个闭集$F\subset \mathbb{R}$使得$|\mathbb{R} - F|<\varepsilon$，而且$g\vert_F$是$F$上的连续函数

注意：这里已经把“可测”指明了是“Borel可测”，即：明确了$\sigma$代数。所以调用之前的定理时，多带一个Borel前缀

证明：先挑软柿子捏，证明$g$是一个简单函数时成立。成功了以后，结合定理“用简单函数逼近可测函数”解决整个问题

1. 若$g= d_1\chi_{D_1}+ d_2\chi_{D_2}\dots d_n\chi_{D_n}$：

那么，根据定理“lebesgue可测集的等价定义”，可以为每一个$D_k$都找到开集$G_k$与闭集$F_k$挨着它，满足$F_k\subset D_k\subset G_k$且$\vert G_k-D_k\vert <\frac{\varepsilon}{2n}$以及$\vert D_k-F_k \vert <\frac{\varepsilon}{2n}$ 因此，$\vert G_k-F_k \vert<\frac{\varepsilon}{n}$

最后，令$F = \bigcup\limits_{k=1}^n F_k \cup \bigcap\limits_{k=1}^n (\mathbb{R} - G_k)$，就ok了！为什么呢？原因有二：第一，这个$F$很大，$\vert\mathbb{R} - F\vert = \vert \bigcup\limits_{k=1}^n (G_k-F_k)\vert <\varepsilon$；第二，因为在$g\vert _ {F _ k}$根本是常值函数，当然连续，因此$g\vert_F$连续（由于$F$为$F_k$们的无交并，易验证合并起来连续）

2. 讨论一般情形，$g$用简单Borel可测函数序列$g_1,g_2,\dots$逼近

首先，调用1的结论，可知对于每一个固定的$k$，都能找到一个闭集$C_k$使得$\vert \mathbb{R}-C_k\vert<\frac{\varepsilon}{2^{k+1}}$而且$g _ k\vert_{C _ k}$是连续的。这样，记$C = \bigcap \limits_{k=1}^\infty C_k$，这样的$C$仍是一个闭集且很大：$\vert\mathbb{R} -C\vert <\frac{\varepsilon}{2}$

欲得$g$的连续性，使用熟知的定理“一致收敛的连续函数序列，其极限连续”，企图让$g_k$序列一致连续。但是一致连续又是从哪来的呢？可以利用Egorov定理！这下，思路就全建立好了

先用Egorov定理：把实轴分成一段一段的，由于$g_k\vert_{(m,m+1)}$是连续的且逐点收敛到$g\vert_{(m,m+1)}$，因此存在一个Borel可测的集合$E_m\subset(m,m+1)$使得$g_k$序列在其上是一致收敛到$g$的，满足$\vert (m,m+1) - E_m\vert< \frac{\varepsilon}{2^{\vert m\vert+3}} $这样的好处是，$\vert \bigcup\limits_{m\in \mathbb{Z}} ((m,m+1)-E_m)\vert \leq \frac{3\varepsilon}{8}$

至此，$\set{g _ k \vert _ {C\cap E _ m }} _ k$这个序列，不仅每一项是连续的，而且还是一致收敛的，经典的“一致收敛+连续$\to$连续”，得到$g\vert _ {C\cap E _ m}$是连续的

全实轴的$g\vert_{C\cap E_m}$联合起来！得到$g\vert_{\bigcup (C\cap E_m)}$也是连续的。这是因为，$g$限制在闭包互不相交的集合上都是连续的，那么这些集合并起来，$g$在其上仍然连续（可以用$\varepsilon/\delta$语言，也可以用拓扑空间的语言证）

但$\bigcup (C\cap E_m)$还不是闭集，不过显然是Borel集，整个证明还差临门一脚，利用定理“lebesgue可测集的等价定义”，存在一个闭集$F$比它小但又和它很接近（$\vert \bigcup (C\cap E_m)-F \vert<\frac{\varepsilon}{8}$），这个$F$就是所求

验证一下： $\vert \mathbb{R} - F\vert = \vert\left(\mathbb{R}-\bigcup (C\cap E_m) \right)\cup \left(\bigcup (C\cap E_m)-F \right)\vert \leq \vert \mathbb{R}-\bigcup (C\cap E_m) \vert + \vert \left(\bigcup (C\cap E_m)-F \right)\vert $

上式中第一项，可回溯构造过程，发现其大小不超过整数点集合$\mathbb{Z}$，并上$\bigcup\limits_{m\in \mathbb{Z}} ((m,m+1)-E_m)$，再并上$\mathbb{R}-C$。因此，$\vert \mathbb{R}-\bigcup (C\cap E_m) \vert \leq 0+ \frac{3\varepsilon}{8} +\frac{\varepsilon}{2}=\frac{7\varepsilon}{8}$

上式第二项又小于$\frac{\varepsilon}{8}$，因此$\vert\mathbb{R} - F\vert\leq \varepsilon$

$\square$

Version 2

这个版本的Luzin定理，说的是这件事：把一个Borel可测的函数，做个“微型手术”（在任意小的集合里里改动一下）就能拓展成一个$\mathbb{R}\to\mathbb{R}$的连续函数

首先来看一个熟悉的引理：

定理 （Tietze扩张）
若$F$是$\mathbb{R}$的闭子集，且$g:F\to\mathbb{R}$是连续的。那么，存在一个连续函数$h:\mathbb{R}\to\mathbb{R}$，使得$h\vert_F = g$

这就是熟知的Tietze扩张定理，在实轴上的特殊版本（比一般情形的好证多了）。欲证明该实轴版本，只用把$\mathbb{R}-F$表示成无交开区间之并，每个开区间中，用一次函数架桥连接左右端就行了

有了这个引理，思路就很清楚了：我们只用先把原本的函数改造成定义域在闭集上的连续函数，再用该引理扩张就行！

定理 （Luzin ver.2）
设$E\subset \mathbb{R}$且$g:E \to \mathbb{R}$是Borel可测的函数，那么对任意$\varepsilon>0$，均可以找到闭集$F\subset E$满足$\vert E-F\vert<\varepsilon$以及一个连续函数$h$，使得$h\vert_F = g\vert_F$成立

先把函数$g$拓展成$\tilde{g}$满足：

$$
\tilde{g}(x) = \begin{cases}
g(x) & x\in E \\
0 & x\in \mathbb{R}-E \\
\end{cases}
$$
那么，容易验证这是Borel可测函数（稍稍分类一下），因此可以用Luzin定理ver.1，得知有一个闭集$C\subset\mathbb{R}$使得$\vert\mathbb{R} -C\vert<\frac{\varepsilon}{2}$且$\tilde{g}\vert_C$连续

由于$C\cap E$是一个Borel集，根据定理“lebesgue可测集的等价定义”，存在一个闭集$F\subset C\cap E$，满足$\vert C\cap E - F\vert< \frac{\varepsilon}{2}$

因此，$\vert E-F\vert \leq\vert C\cap E-F \vert+\vert \mathbb{R}-C \vert <\varepsilon$

这样，$g\vert_F$就是一个定义在闭集上的连续函数，调用定理（Tietze扩张）即可把$g\vert_F$扩展到$h:\mathbb{R}\to\mathbb{R}$，即为所求

$\square$