统计学习方法
决策树
简介
决策树由结点和有向边组成,最末端的叶结点表示一个类
非末端的结点就是一个决策点,类似于switch case语句,经过该决策点后数据就做了一次划分。整棵树,就是一些case语句的合体
我们要通过一些数据,学出一颗棵很聪明的树,能对新来的数据进行分类,企图让树拥有决策的智慧
十年树木,百年树人
目标:我们需要的是一个与训练数据矛盾较小的树,而不是一个完美划分的树,如果目标是完美划分,那么树很可能非常“长条状”,而且泛化能力弱。但实际上我们想要的是结构精简的一颗矮的树,有较强的泛化能力
为什么“长条”的树不好?因为我们想要的是反映核心结构的决策,能够根据一些内在的逻辑进行决策,比如下图:
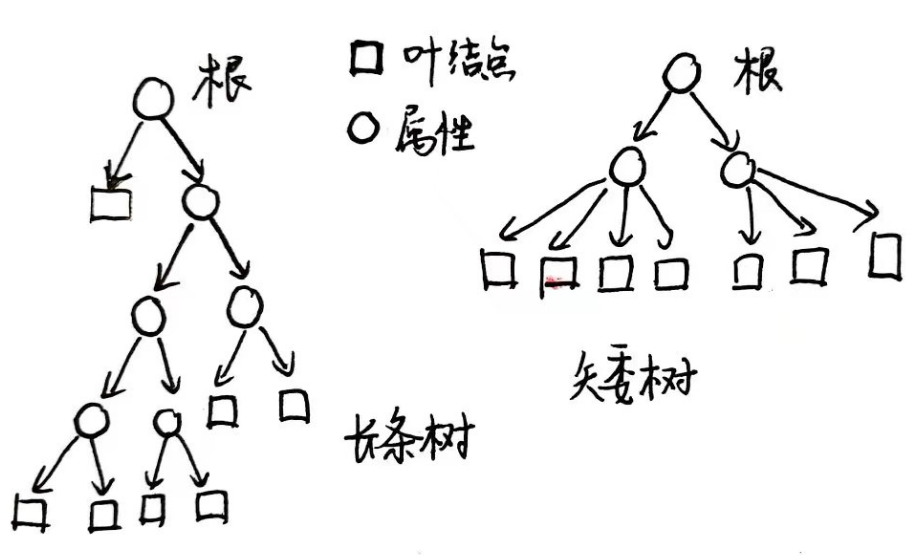
同样是分七类,右边的树之所以讨人喜欢,是因为它才依靠三个特征就把所有实例分类好了,它抓住了问题的关键,左边的树则明显没弄清楚核心,先处理了一些细枝末节的信息
增益其所不能
如果某个特征能起决定性作用,那么把它安排在决策的第一步,能够更快结束分类;但是有些不重要的特征,拿它做分类,起的效果和随机乱猜差不多,那它根本没什么用。这就是两个特征在信息增益方面的差异
设想一个过程:手中拿到了一些数据点:
| 类别 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
|---|
在一开始,还不知道任何关于它的特征,怎么将其正确分类呢?既然没有任何特征的信息,唯一的方法就是按照每一类出现次数的多少,得知经验频率。若10个数据点中,第一类出现了3次,第二类出现2次,第三类出现5次,那么经验上就觉得三类概率为0.3,0.2,0.5,这样就对于目前的数据的不确定性有了一种定量的描述,可以算出“经验”熵:
$$
H(D)=-0.3\log 0.3-0.2\log 0.2-0.5\log 0.5
$$
倘若我们又进一步得到了某一个特征$A$的信息如下:
| 类别 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| A特征 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
在这个信息的帮助下,理应减少一些“不确定性”:直觉来说,如果$A$特征是1,那么很可能是第一类,反之很可能是第三类;定量来说,在“已知$A$的条件下”,“不确定”就应该用条件熵描述,变成:
$$
\begin{align*}
H(D|A)&=0.4 H(D|A=1)+0.6 H(D|A=0)
\newline
&=0.4 (-\frac{3}{4}\log \frac{3}{4}-\frac{1}{4}\log\frac{1}{4})+0.6 (-\frac{1}{6}\log\frac{1}{6}-\frac{5}{6}\log \frac{5}{6})
\end{align*}
$$
这下就从$H(D)$到了$H(D|A)$,熵变小的程度就是信息增益:
$$
g(D,A)=H(D)-H(D|A)
$$
当然如果知道的是另外一个特征$B$,它也带来一个信息增益$g(D,B)$,谁的信息增益最大,说明谁对“不确定性”的消除最多,谁就应该作为首选的分类特征
(不过,上段的最后一句话不全对,有时是拿信息增益比而不是信息增益来判断谁作为首选)
形式化描述
数据集$D$,类别有$K$个,分别为$C _ k$,$|C _ k|$就表示这类里有几个数据点。特征$A$的取值有$\set{a _ 1,a _ 2,\dots,a _ n}$,特征取$a _ i$的数据的集合为$D _ i$,$\set{D _ i} _ i$就是原始数据的一种分划。在$D _ i$中,属于$C _ k$类的样本集合记为$D _ {ik}$,其中元素$|D _ {ik}|$个
原始的经验熵:
$$
H(D)=-\sum_{k=1}^K \frac{|C_k|}{|D|}\log \frac{|C_k|}{|D|}
$$
考虑$A$后,新的不确定度变成:
$$
H(D|A)=\sum_{i=1}^n \frac{|D_i|}{|D|}H(D_i)=\sum_{i=1}^n \frac{|D_i|}{|D|}\left( -\sum_{k=1}^K \frac{|C_{ik}|}{|D_i|}\log \frac{|C_{ik}|}{|D_i|}\right)
$$
信息增益就是二者之差:
$$
g(D,A)=H(D)-H(D|A)
$$
信息增益比则是(分母可以说是“把特征视为数据后的经验熵”):
$$
g_R(D,A)=\frac{H(D)-H(D|A)}{-\sum_{i=1}^n \frac{|D_i|}{|D|}\log \frac{|D_i|}{|D|}}
$$
学出一棵树需要几步
(和把大象装进冰箱一样,都只用三步)
现已拿到拥有特征的训练数据集,记全体特征的集合为$A$
ID3算法如下:
对于该数据集,算出各个特征的信息增益,增益最大的那个特征记为$A_g$,作为首选特征
根据$A_g$把原始数据划分为多个子集
每个子集都视为全新的数据集,只不过特征少了,变成$A-\set{A_g}$,递归调用第1步
至于停止条件,可以事先设定一个信息增益的阈值$\epsilon$,若信息增益小于它了,那就停止;也有可能,已经把所有特征都用完了,还是没分好,那不得不结束(为什么会这样呢?设想有两个数据,所有特征取值都一模一样,但类别竟然不一样,这是训练数据自身出矛盾了,巧妇难为无米之炊)
C4.5算法,就是把ID3中的“信息增益”换成“信息增益比”,其余一模一样
修枝剪叶
按照刚才的算法的确会生成一棵树,但是这棵树还是可能太复杂,即叶结点太多了,很多时候,末端那里不用分那么细,所以可以剪叶:
定义损失函数:
$$
C_\alpha = -\sum_k \frac{N_{kt}}{N_t}\log \frac{N_{kt}}{N_t} +\alpha|T|
$$
$C_\alpha$的第一部分,是“错分”的表征,其中$N_t$代表第$t$个叶结点,而$N_{kt}$是其中第$k$类的个数,理想情况,每一个叶结点就是一类,那么这一部分取对数后就是0,但如果叶结点鱼龙混杂,那这一项就会比较大,以示惩罚
第二部分,$\alpha\geq 0$是你自己定的一个参数,$|T|$就是一共有的叶结点数量,说明结构越复杂(叶子越多),越要惩罚
如何修剪刚才(比如ID3)生成的树呢?选定一个叶结点,回缩到它上面一层的父节点,幻想:如果分到这个父结点为止就停了,不就能得到一棵更简单的树嘛!这棵简单的树和原来的树仅在这一个区域不同,比较一下谁的损失函数更小,如果简单的树更小,那就采纳简单的树,效果就像把叶结点剪掉了一样
简单的树的优势在于,$\alpha|T|$比较小,而原来那棵树的优势在于分的比较细,因此$-\sum_k \frac{N_{kt}}{N_t}\log \frac{N_{kt}}{N_t}$比较小,权衡利弊,修剪与否




