Complex Analysis

基本概念

Holomorphic

如果$f(z)$在开集$U$中固定每一个点都可微，则称$f$在$U$上是全纯的（holomorphic）

保角性质（conformal）：

如果$f’(z_0)\neq 0$，那么曲线$\gamma,\eta$在$z_0$点的夹角和$f \circ \gamma$与$f\circ \eta$在$f(z_0)$的夹角是一样的

积分

Local Primitive

先明确概念：称一个函数在任意一个集合$R$上全纯，其实指的是存在一个包含$R$的大的开集，而$f$在这个大的开集中全纯

定理 Goursat $R$是复平面中一个闭矩形，而$f$是一个在$R$上全纯的函数，那么
$$
\int_{\partial R}f=0
$$

证明

只需证$|\int_{\partial R} f|\leq 0$，所以先放大这个积分

把矩形$R$一分为四，原积分变成四个环路积分叠加，中间重边相消。总有一个环路积分的模值最大，记这个环路为$\partial R^{(1)}$，这带来不等式：
$$
\frac{1}{4}|\int_{\partial R} f|\leq |\int_{\partial R^{(1)}} f|
$$
对$R^{(1)}$重复此操作，之后再不断重复，生成一个可数长方形序列，有：
$$
\frac{1}{4^n}|\int_{\partial R} f|\leq |\int_{\partial R^{(n)}} f|
$$

所有长方形点集的交集只有一个点（因为完备且闭），记为$z_0$

令$f(z)=f(z_0)+f’(z_0)(z-z_0)+(z-z_0)h(z)$（因为$f(z)$在$z_0$点可微，因此该式合理），且根据可微的定义，$\lim\limits_{z\to z_0}h(z)=0$，因此

$$
\int_{\partial R^{(n)}} f = \int_{\partial R^{(n)}} f(z_0)dz + f’(z_0)\int_{\partial R^{(n)}} (z-z_0) dz+\int_{\partial R^{(n)}}(z-z_0)h(z) dz
$$
前面两项，在任意的集合中都可以找到全纯原函数（primitive），积分为零，只剩下最后一项：

$$
\frac{1}{4^n}|\int_{\partial R} f|\leq |\int_{\partial R^{(n)}} (z-z_0)h(z) dz|\leq \text{diam}R^{(n)} \sup|h(z)| L_n
$$
其中，$\text{diam} R^{(n)}$是$(z-z_0)$放大的结果，指的是$R^{(n)}$中的最远的两点距离的上确界，因此$=\frac{1}{2^n}\text{diam} R$；$L_n$指的是$R^{(n)}$环路周长，因此和原始的$R$的周长$L$有联系$L_n=\frac{1}{2^n}L$。上式即为：
$$
|\int_{\partial R} f|\leq \text{diam}R \sup|h(z)| L
$$
用一下$\lim\limits_{z\to z_0}h(z)=0$，右边为零，得证

定理 Existence of Local Primitive：在上方定理的帮助下，可通过构造的方法，证明开圆盘中一个全纯函数存在原函数（$z_0$是圆盘中心），构造如下：
$$
g(z_1):=\int _{z_0}^{z_1} f
$$
其中这个路径规定是从圆心$z_0$出发，横着走和竖着走到$z_1$（否则得不到Goursat的帮助）

证明提要：只要证一下$\lim\limits_{h\to 0}\frac{g(z_1+h)-g(z_1)}{h}$存在，且等于$f(z_1)$

Integral — Another Interpretation

另一个有趣的积分理解建立在“局部原函数”的基础上：

对于一个曲线$\gamma: [a,b]\to U$，可构造一个划分（partition）为：$a=a_0\leq a_1\leq\dots\leq a_n=b$，由于$\gamma\in C^1$，且定义在闭区间上，因此一致连续，有效果“只要划分够细$|a_i-a_{i+1}|< \delta$，像点就够近$|\gamma(a_i)-\gamma(a_{i+1})|< \epsilon/2$”

既然像点够近，就可以拿一个圆心在$\gamma(a_i)$，半径为$\epsilon$的开圆盘包裹住下一个点$\gamma(a_{i+1})$，对于每一个$a_i$都能如此操作（当然，能找到$\epsilon$使得圆盘不会超出$U$的范围是易论证的）

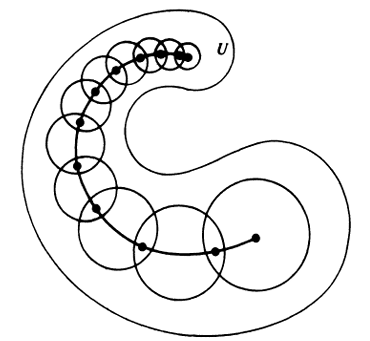
按照这个方法，可以构造出一系列衔接的开圆盘，从曲线的一头$\gamma(a)$架桥到另一头$\gamma(b)$

看看每个小圆盘，之前的“圆盘中全纯函数的原函数存在”不就在这里用上了嘛！即使$f$全局的原函数并不存在，但积分还是能算：因为每一个小圆盘里原函数存在，故每两个划分点之间一小段的积分值都可以算，它们累加起来，就是沿着整个曲线积分的值

其实，这就可以视为曲线积分的一种定义（用局部的原函数定义曲线积分），当然，为了验证这种定义是well-defined，还需要检查划分的选取和圆盘的选取不会影响积分值

Two Lemmas

定理 Close Together 两个都定义在$[a,b]$中，共起点与终点，且“挨得很近”的曲线，全纯函数$f$在它们上的曲线积分值是一样的：

$$
\int_\eta f=\int_\gamma f
$$

这是“挨得很近”的定义：存在区间$[a,b]$的某一个划分$a=a_0\leq a_1\leq\dots\leq a_n=b$，在两个曲线上对应的每一段，即$\gamma([a_i,a_{i+1}])$与$\eta([a_i,a_{i+1}])$，都能包裹在同一个架桥圆盘$D_i$中，就称之为“挨得很近”

按照上一节中曲线积分的定义分别算一下两个积分，两者都是同一个值，即$g_{n-1}(\gamma(b))-g_0(\gamma(a))$（其中，$g_i$代表在$D_i$中的局部原函数）

同样有

定理 Close Together 两个都定义在$[a,b]$中，且“挨得很近”的闭合曲线，全纯函数$f$在它们上的曲线积分值是一样的

Homotopy

同伦（homotopy）是曲线塑性的艺术，定义如下：

两个道路（path，即多段曲线相连）$\eta$与$\gamma$都定义在$[a,b]$上，称它们是同伦的，如果存在一个连续函数$\psi :[a,b]\times[c,d]\to U$，使得：$\psi(t,c)=\gamma(t)$，$\psi(t,d)=\eta(t)$，对于$\forall t\in [a,b]$成立

可以看出，第一个变量$t$就是一条曲线的参数变量，而第二个变量$\in [c,d]$则是一个塑性变量，决定曲线的形状

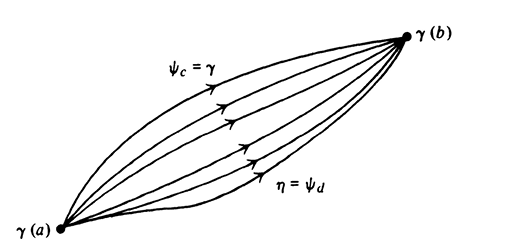
如上图，这么多曲线就是因为塑性参数的变化而生成的

由于$\psi$是连续，因此这种塑性也是橡皮泥一样连续的塑性，这说明：塑性参数变化一点点，带来形状的变化也是微小的，变化前后两条曲线“挨得很近”，这样，两个引理就有用武之地：

定理 Homotopic functions’ Integral 令在开集$U$上定义的两个闭合道路$\eta$与$\gamma$是同伦的，则对于全纯函数$f$：
$$
\int_\gamma f=\int_\eta f
$$

证明：
根据“紧+连续”，知$\psi$也是一致连续的，这样子，只要划分够细：$a=a_0\leq a_1 \dots\leq a_n=b $以及$c=c_0\leq c_1\dots \leq c_n=d$满足两个分点距小于某个$\delta$，那么就有：

$$
S_{ij}=[a_i,a_{i+1}]\times [c_j,c_{j+1}] \quad \psi(S_{ij}) \subset D_{ij}
$$
其中$D_{ij}$是架桥小圆盘，那么，$\psi_{c_j}(t)=\psi(t,c_j)$以及$\psi_{c_{j+1}}=\psi(t,c_{j+1})$就是“挨得很近”的，引用前面的引理之一，即得
$$
\int_{\psi_{c_j}} f=\int_{\psi_{c_{j+1}}} f
$$
然后随着$j$的变化，即可知随着塑性参数的变化，积分不变，得证

同样平行的有（只不过证明中用了另一个引理）：

定理 Homotopic functions’ Integral 令在开集$U$上定义的两个同起始点与终点的道路$\eta$与$\gamma$是同伦的，则对于全纯函数$f$：
$$
\int_\gamma f=\int_\eta f
$$