click here to save the pdf version of this article
Mathematical Physics
Partial Differential Equation
The Classes of PDE
We only discuss PDE with two variables.
Basic PDE Example
What matters is to find the characteristics of a PDE (constant coefficient):
$$
\mathcal{L}(u)=0
$$ where $$
\mathcal{L}=a\frac{\partial^2 }{\partial x^2}+2b\frac{\partial^2 }{\partial x\partial y}+c\frac{\partial^2 }{\partial y^2}
$$
If we find the characteristic, then the equation become single variable equation of the characteristic.
To achieve this, we factorize the above equation:
$$
\mathcal{L}=\left(\frac{b+\sqrt{\Delta }}{c^{1/2}}\dfrac{\partial }{\partial x}+c^{1/2}\dfrac{\partial }{\partial y}\right) \left(\frac{b-\sqrt{\Delta }}{c^{1/2}}\dfrac{\partial }{\partial x}+c^{1/2}\dfrac{\partial }{\partial y}\right)
$$
where $\Delta:=b^2-ac$
Note that the two factors are commutative, hence if $\Delta\neq 0$, the two factors implies two characteristics separately.
If $\Delta =0$, there’s only one characteristic line.
And the characteristic is given by
$$
\frac{dy}{dx}=\frac{b\pm \sqrt{\Delta}}{a}
$$
Because any $x, y$ with this relation (i.e. $y(x)$) would imply $\mathcal{L}=0$ and the $u(x,y)$ actually becomes $u(x,y(x))$, single valued.
To achieve the canonical form of the second order PDE, we import such variables:$\xi=\sqrt{c}x-\frac{b}{\sqrt{c}}y;\eta =\frac{1}{\sqrt{c}}y$.
$$
\mathcal{L}=\left(\frac{b+\sqrt{\Delta }}{c^{1/2}}\sqrt{c}\frac{\partial }{\partial \xi}+c^{1/2}\frac{-b}{\sqrt{c}}\frac{\partial }{\partial \xi}+c^{1/2}\frac{1}{\sqrt{c}}\frac{\partial}{\partial \eta}\right)\times
$$
$$
\left(\frac{b-\sqrt{\Delta }}{c^{1/2}}\sqrt{c}\frac{\partial }{\partial \xi}+c^{1/2}\frac{-b}{\sqrt{c}}\frac{\partial }{\partial \xi}+c^{1/2}\frac{1}{\sqrt{c}}\frac{\partial}{\partial \eta}\right)
$$
$$
=\left(\sqrt{\Delta}\frac{\partial}{\partial \xi}+\partial \eta \right)\left(-\sqrt{\Delta}\frac{\partial}{\partial \xi}+\partial \eta \right)=-\Delta \frac{\partial^2}{\partial \xi^2}+\frac{\partial^2}{\partial \eta^2}
$$
Systematic Process
The equation is:
$$
\mathcal{L}(u)=g
$$ where:
$$
\mathcal{L}=a\frac{\partial^2 }{\partial x^2}+2b\frac{\partial^2 }{\partial x\partial y}+c\frac{\partial^2 }{\partial y^2}+d\frac{\partial }{\partial x}+e\frac{\partial }{\partial y}+f
$$
Attention: $a$ to $g$ are all functions of $x$ and $y$, they’re not constant generally.
Replacing the variables by:
$$
\xi =\xi (x,y) \quad \eta=\eta (x,y)
$$
Apply Chain Rule and calculate, we got:
$$
\left(A\frac{\partial^2 }{\partial \xi^2}+2B\frac{\partial^2 }{\partial \xi\partial \eta}+C\frac{\partial^2 }{\partial \eta^2}+D\frac{\partial }{\partial \xi}+E\frac{\partial }{\partial \eta}+F\right)(u)=G
$$
where $A$ and $C$ have the same form:
$$
a(\frac{\partial W}{\partial x})^2+2b\frac{\partial W}{\partial x}\frac{\partial W}{\partial y}+c(\frac{\partial W }{\partial y})^2
$$
In $A$’s case $W=\xi$, in $C$’s case $W=\eta$.
Suppose the solution is $W(x,y)=\text{const}$, then by Implicit Function theorem, $y’=-\frac{\partial W / \partial x}{\partial W / \partial y}$, so that the equation above will be:
$$
a{y’}^2-2by’+c=0 \qquad\therefore y’=\frac{b\pm \sqrt{\Delta}}{a}
$$
If you successfully solve the last differential equation we got $\xi(x,y)=\text{const}$ and $\eta(x,y)=\text{const}$, which are exactly two characteristics.
If there are two solutions and they are real, that’s typical hyperbola type equation, hence we get:
$$
\frac{\partial^2 u}{\partial \xi\partial \eta}=\dots
$$
or you may as well adjust it to $\frac{\partial^2 u}{\partial \alpha^2}-\frac{\partial^2 u}{\partial \beta^2}=\dots$ by letting $\alpha=\frac{1}{2}(\xi+\eta)$ and $\beta=\frac{1}{2}(\xi-\eta)$.If there’s only one solution (i.e. parabolic), then another characteristic can be chosen by yourself, as long as it’s independent with the previous one. The one you chose randomly namely is $\eta$, then the equation be like:
$$
\frac{\partial^2 u}{\partial \eta^2}=\dots
$$If the solutions $\notin \mathbb{R}$, then extract the $ W$ ‘s real and imaginary part to be $\xi$ and $\eta$ separately. (it can be proved by simply plugging in that such arrangement is indeed the appropriate solution) And we get elliptical equation:
$$
\frac{\partial^2 u}{\partial \xi^2}+\frac{\partial^2 u}{\partial \eta^2}=\dots
$$
D’Almbert Method
To solve the vibrating equation:
$$
\frac{\partial^2 u}{\partial t^2}-a^2\frac{\partial^2 u}{\partial t^2}=0
$$
written as
$$
(\frac{\partial }{\partial t}+a\frac{\partial }{\partial x})(\frac{\partial }{\partial t}-a\frac{\partial }{\partial x})u=0
$$
The general solution would be $f_1(x+at)+f_2(x-at)$.
$$
u(x,t)=\frac{1}{2}(\phi(x+at)+\phi(x-at))+\frac{1}{2a}\int_{x-at}^{x+at} \psi(\xi) d\xi
$$
Boundary Condition
Mechanical Example

Consider the example of a rod oscillates longitudinal with a spring sticking to its the end.
Analysis the small segment in Rod’s part: $u(x)$ represents the small displacement at the point $x$, and note rightward as the positive direction. Calculate the new length of the segment:
$$
(x+\Delta x+u(x+\Delta x))-(x+u(x))=\Delta x+ \frac{\partial u}{\partial x}\Delta x
$$ Such that the extension is $\frac{\partial u}{\partial x}\Delta x$. From Hook’s Law, the relative extension is proportional to the quotient of the force and sectional area:
$$
\frac{\frac{\partial u}{\partial x}\Delta x}{\Delta x}=\frac{F}{SY} \quad
\therefore F=SY\frac{\partial u}{\partial x}
$$ Analysis the force to get Dynamic Equation:
$$
SY\left( \frac{\partial u}{\partial x}\left.\right\vert_{x+\Delta x}-\frac{\partial u}{\partial x}\left.\right\vert_{x} \right )=\frac{\partial^2 u}{\partial t^2} \rho S \Delta x
$$
Hence the equation is:
$$
\frac{Y}{\rho} \frac{\partial^2 u}{\partial x^2}=\frac{\partial^2 u}{\partial t^2}
$$
The Boundary Condition shall be given by analyzing the small segment at the end of the rod, adjust the Dynamic Equation above:
$$ F_{x+\Delta x}+SY\left( -\frac{\partial u}{\partial x}\left.\right\vert_{x} \right )=\frac{\partial^2 u}{\partial t^2} \rho S \Delta x
$$ $$
F_{L^+}+SY\left(-\frac{\partial u}{\partial x}\left.\right\vert_{L-\Delta x} \right )=\frac{\partial^2 u}{\partial t^2} \rho S \Delta x
$$ $$
-ku\left.\right\vert_{L}+SY\left( -\frac{\partial u}{\partial x}\left.\right\vert_{L-\Delta x} \right )=\frac{\partial^2 u}{\partial t^2} \rho S \Delta x
$$
Now let $\Delta x\rightarrow 0$, to achieve the final goal:
$$
-ku\left.\right\vert_{L}+\frac{S}{Y}\left( -\frac{\partial u}{\partial x}\left.\right\vert_{L} \right )=0
$$
When $k$ is large enough, the $\frac{S}{Y}\left( -\frac{\partial u}{\partial L}\left.\right\vert_{L} \right )$ part is $o(k)$ and is legal to be ignored, corresponding the situation with fixed end (the first type, Dirichlet Boundary Condition).
When $k$ is small enough, the first section $-ku\left.\right\vert_{L}$ could be ignored and thus verified the Boundary Condition of free end (the second type, Neumann Boundary Condition).
In conclusion, the boundary condition exhibits a lower order of small infinitesimal quantity. At the end of the rod, the $\Delta x$ could be regarded as zero, which differs from the interior of the rod.
Thermodynamical Example
To understand BC, you shall first understand where the equation comes from, for a small fragment of the rod:
$$
\left(-\kappa S \Delta t \frac{\partial u}{\partial x}\right)\vert_{x}-\left(-\kappa S \Delta t \frac{\partial u}{\partial x}\right)\vert_{x+\Delta x}=c(S \Delta x \rho) \Delta u
$$
which can be simplified to
$$
\kappa \frac{\partial^2 u}{\partial x^2}=c\rho\frac{\Delta u}{\Delta t}
$$
For a rod’s temperature distribution, the Dirichlet BC means the temperature was shown directly. If it states that some hot stream $f(t)$ flows out, that’s the Neumann BC, and the general equation at the right end should be:
$$
\left(-\kappa S \Delta t \frac{\partial u}{\partial x}\right)|_{L}-\Delta t Sf(t)=c(S \Delta x \rho) \Delta u
$$
Eliminate $\Delta t$ and let $\Delta x\to 0$,
$$
-\kappa \frac{\partial u}{\partial x}|_{x=L}=f(t)
$$
or more generally
$$
-\kappa \frac{\partial u}{\partial n}=f(t)
$$
where at the left end, $\frac{\partial u}{\partial n}=-\frac{\partial u}{\partial x}$, while at the right end $\frac{\partial u}{\partial n}=\frac{\partial u}{\partial x}$, the normal $\vec{n}$ is pointing outward of the rod!
When the end is adiabatic, the BC becomes $\frac{\partial u}{\partial n}=0$.
There’s another possibility that the boundary obeys Newton’s cooling law, which corresponds to the spring in above mechanical example, because the $\text{force} \propto \Delta \text{displacement}$ corresponds to $\text{flow}\propto \Delta\text{temperature}$.
thus the BC:
$$
-\kappa\frac{\partial u}{\partial n}\vert_{\text{somewhere}} = h(u\vert_{\text{somewhere}}-\theta)
$$
Different Types, Different Methods
Homogenous BC and Homogenous Eq
The easiest one, Separate two variables to get an eigen-value problem.
Homogenous BC and Non-Homogenous Eq
There are two ways to deal with it:
Fourier method
Suppose:
$$
u(x,t)=\sum_{n=1}^{\infty}T_n(t)X_n(x)
$$
where $X_n(x)$ is the eigen-function which we already know, corresponding to BC, like $\sin(\frac{n\pi}{l}x)$. Plug the above formula into the original Eq to derive $T_n(t)$’s differential equation and solve that ode.
Momentum Theorem
To implement Momentum Theorem, we have to convert the original Eq to the following form, with all zero Initial Condition, if it’s a Vibrating Equation:
$$
u_{tt}-a^2 u_{xx}=f(x,t)
$$
$$
u\vert_{x=0}=0 \quad u\vert_{x=l}=0
$$
$$
u\vert_{t=0}=0 \quad u_t\vert_{t=0}=0
$$
Then we only need to solve:
$$
v_{tt}-a^2 v_{xx}=0
$$
$$
v\vert_{x=0}=0 \quad v\vert_{x=l}=0
$$
$$
v\vert_{t=\tau}=0 \quad v_t\vert_{t=\tau}=f(x,\tau)
$$
If it’s the thermodynamical equation
$$
u_{t}-a^2 u_{xx}=f(x,t)
$$
$$
u\vert_{x=0}=0 \quad u\vert_{x=l}=0
$$
$$
u\vert_{t=0}=0
$$
Then we only need to solve:
$$
v_{t}-a^2 v_{xx}=0
$$
$$
v\vert_{x=0}=0 \quad v\vert_{x=l}=0
$$
$$
v\vert_{t=\tau}=f(x,\tau)
$$
and the final result is:
$$
u(x,t)=\int_0^t v(x,t,\tau) d\tau
$$
Understanding:
The $f(x,t)$ shall be divided into discrete impulses, exerted on different strings (in an ensemble), and the result is the sum of all strings in this ensemble.
Non-Homogenous BC and Homogenous Eq
The goal is to regain homogenous BC and convert it to the last type of equation.
Let $u=v+w$, where $w$ satisfy homogenous BC. To achieve this, suppose $v=A(t)x+B(t)$, and adjust two coefficients to satisfy the non-homogenous BC. As a side-effect ,$w$ has to satisfy the non-homogenous equations but we already know how to solve it.
Poisson function
The form is:
$$
\Delta u=f(x,y,z)
$$
non-homogenous equations, unfortunately not able to solve by Momentum theorem. Thus we have to develop new method:
Guess! Extract a particular solution out, $u=v+w$ transferring the equation into a homogenous one $\Delta v=0$. Separate variables……
Note that if the Poisson function is a two dimensional problem with variables $x$ and $y$, the BC must be fine or else we cannot determine its eigen-function (as you extract a particular solution out and worsen the BC).
While if the variables are $\rho$ and $\phi$, the solution $w$ you extract must have the sysmetric form in terms of $x$ and $y$, in order to combine it to $x^2+y^2=\rho^2$, by the way, you will probably encounter Euler type ode then.
tips: when encounter Euler type ode, let $\rho=e^t \dots$. The general solution would be like:
$$
v(\rho,\phi)=\sum_{m=1}^\infty \rho^{m}(A_m \cos m\phi+B_m\sin m\phi)
+C_0+D_0\ln \rho+\sum_{m=1}^\infty \rho^{-m}(C_m \cos m\phi+D_m\sin m\phi)
$$
Solve ODE a Hard Way
Sturm-Liouville Problem
Consider the operator:
$$
\mathcal{L}y=\frac{d}{dx}\left(p_0(x)\frac{dy}{dx} \right)+p_2(x)y
$$
It is Hermitian in differential equation sense, because for two functions of $x$ denote as $v$ and $u$:
$$
\int_a^b v^* (\mathcal{L}u) dx=\int_a^b (\mathcal{L}v)^* u dx+\left[ v^* p_0(x) \frac{d u}{dx}- \frac{d v^*}{dx} p_0(x) u\right]_{a}^{b}
$$
where the $[\dots]$ term would vanish when the boundary condition is appropriate.
An Hermitian operator enable us to gain orthogonal, complete basis consisting of eigen-functions with real eigenvalues.
Besides, for an arbitrary ode:
$$
\mathcal{L}y=\frac{d^2 y}{dx^2}+a(x)\frac{dy}{dx}+b(x)y
$$
multiply by $e^{\int a(\xi)d\xi}$ (denote as $w(x)$).
$$
w(x)\mathcal{L}y=\frac{d}{dx}\left[e^{\int a(\xi)d\xi}\frac{dy}{dx}\right]+\left[b(x)e^{\int a(\xi)d\xi}\right]y
$$
successfully transform into a S-L type. But note that the orthogonality might be different:
$$
\int_a^b v^* (w(x)\mathcal{L}u) dx=\int_a^b (w(x)\mathcal{L}v)^* u dx+\left[ v^* w(x) \frac{d u}{dx}- \frac{d v^*}{dx} w(x) u\right]_{a}^{b}
$$
Legendre Equation
$l$ th order Legendre Eq:
$$
(1-x^2)y’’-2xy’+l(l+1)=0
$$
Frobenius method by making a series expansion, note that at $x_0=0$ the expansion has only positive terms, i.e. Taylor expansion:
$$
y=\sum_{n=0}^{\infty}a_nx^n
$$
plug it in and get the recursion relation:
$$
a_{k+2}=\frac{(k-l)(k+l+1)}{(k+2)(k+1)} a_k
$$
The general solution:
$$
y(x)=D_0y_0(x)+D_1y_1(x)
$$
A sad fact is that neither $y_0$ nor $y_1$ is convergent, which can be verified by applying Gaussian Criteria:
Gaussian Criteria
the infinite series is $\sum u_k$, denote $$G:=\lim_{k\to \infty} k\left(\frac{u_k}{u_{k+1}}-1-\frac{1}{k}\right)$$
If $G<1$, the series converges; else if $G>1$, it diverges.
Proof: The theorem could be verified by consider $\sum \frac{1}{k\ln k}$
Besides the linear combination of these two diverges too.
The only solution to fit the real physical situation (avoid infinity) is to convert the infinite series into a polynomial (legendre polynomial).
when $l=2n$, $y_0(x)$ is an $2n$ th order polynomial, while $y_1(x)$ is still infinite, thus we assert $a_1=0$ to discard it. The solution shall be $y(x)=a_0 y_0(x)$.
when $l=2n+1$, $y_1(x)$ is an $2n+1$ th order polynomial. Then we abandon $y_0(x)$ to get the solution $y(x)=a_1 y_1(x)$.
Bessel Equation
$$
x^2y’’+xy’+(x^2-\nu^2)y=0
$$
The simple case
where $2\nu \notin \mathbb{Z} $
suppose
$$
y=\sum_{k=0}^{\infty} a_k z^{s+k}
$$
In convention we select $a_0\neq 0$
the $x^s$ term’s coefficient is $(s^2-\nu^2)a_0$, which yields $s=\nu$ or $s=-\nu$
thus the recursion relation is:
$$
a_k=\frac{-1}{(s+k+\nu)(s+k-\nu)}a_{k-2}
$$
Besides, the $x^{s+1}$ term’s coefficient implies $a_1=0$, thus $a_{2k+1}=0$
A great property of Bessel Eq’s solution is that its convergent radii is $\infty$.
select
$$ a_0=\frac{1}{2^\nu}\Gamma(\nu+1) $$
and denote the solution now as $J_\nu (x)$ and $J_{-\nu}(x)$ corresponding to $s=\pm \nu$
$$
J_\nu(x)=\sum_{m=0}^{\infty}\frac{(-1)^m}{m!\Gamma(m+\nu+1)}\left(\frac{x}{2}\right)^{2m+\nu}
$$
$$
J_{-\nu}(x)=\sum_{m=0}^{\infty}\frac{(-1)^m}{m!\Gamma(m-\nu+1)}\left(\frac{x}{2}\right)^{2m-\nu}
$$
They are linear independent, which enables us to form its general solution:
$$
y(x)=C_1 J_\nu(x)+C_2 J_{-\nu}(x)
$$
The 1/2 case
when $\nu=\frac{1}{2}$, the above formula also satisfies.
$$
J_{\frac{1}{2}}(x)=\sqrt{\frac{2}{\pi x}}\sin x
$$
$$
J_{-\frac{1}{2}}(x)=\sqrt{\frac{2}{\pi x}}\cos x
$$
General solution:
$$
y(x)=C_1 J_\nu(x)+C_2 J_{-\nu}(x)
$$
The tough case
$\nu$ is an integer, which implies $J_\nu(x)$ and $J_{-\nu}(x)$ is linear independent.
The first $J_\nu(x)$ still holds, the purpose is to find another solution which is linear independent with it. Neumann function:
$$
Y_\nu(x)=\lim_{\alpha\to \nu}\frac{J_\alpha(x)\cos\alpha x-J_{-\alpha}(x)}{\sin\alpha x}
$$
thus the solution takes the form of:
$$
y(x)=AJ_\nu(x)+BY_\nu(x)
$$
Appendix
Derive the Laplacian $\Delta=\nabla\cdot\nabla$ in a smarter way:
first consider the gradient:
$$
\nabla u =\lim_{\text{Displacement}} \vec{e_r}\frac{\Delta u}{\Delta r}+\vec{e_\theta}\frac{\Delta u}{r\Delta \theta}+\vec{e_\phi}\frac{\Delta u}{r\sin\theta \Delta \phi}
$$
$$
=\vec{e_r}\frac{\partial u}{\partial r}+\vec{e_\theta}\frac{1}{r}\frac{\partial u}{\partial \theta}+\vec{e_\phi}\frac{1}{r\sin \theta}\frac{\partial u}{\partial \phi}
$$
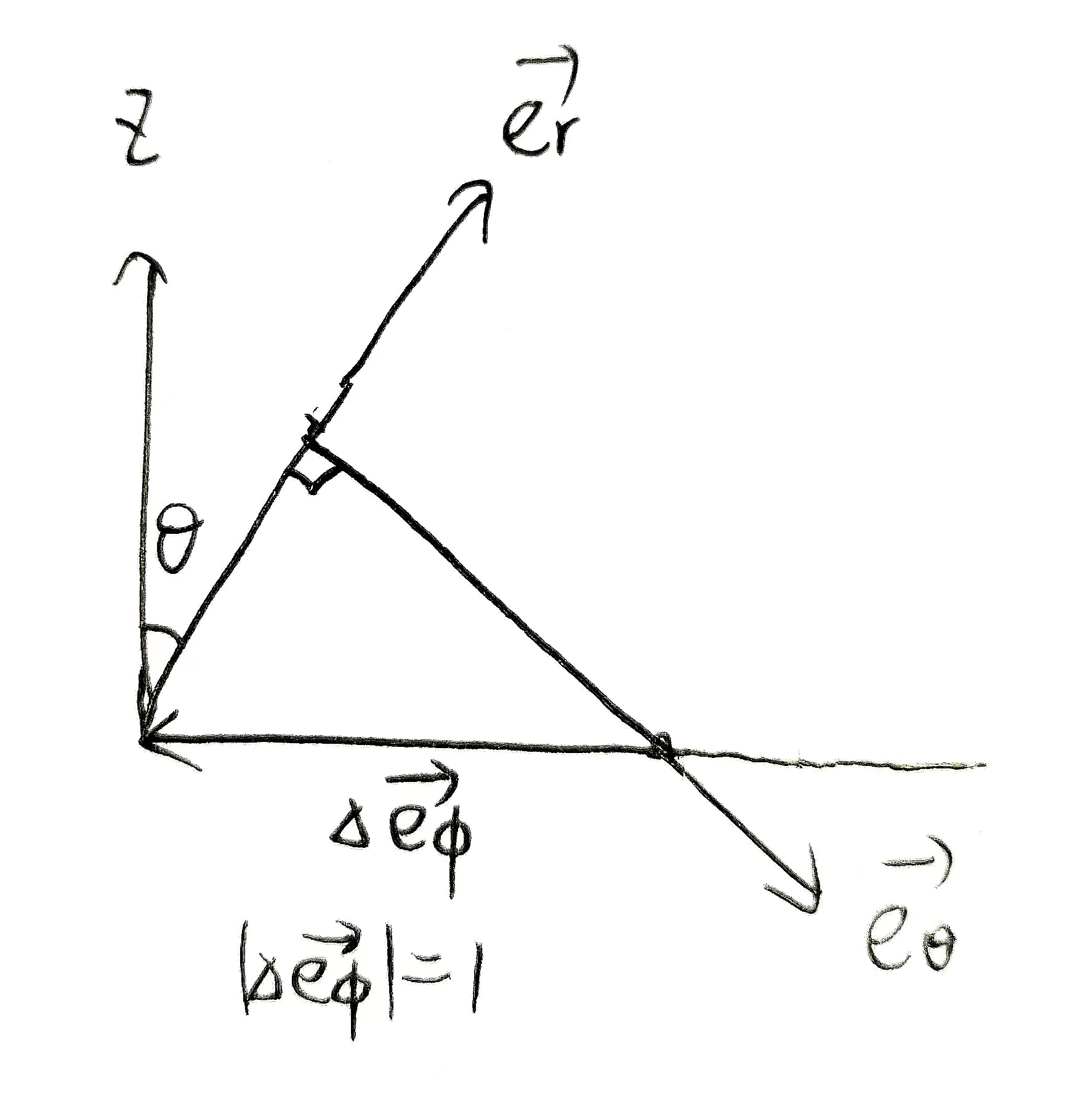
Then consider the partial derivative of the three orthonormal vectors $\vec{e_r}$ $\vec{e_\theta}$ $\vec{e_\phi}$ :
$$
\frac{\partial \vec{e_r}}{\partial r}=\frac{\partial \vec{e_\theta}}{\partial r}=\frac{\partial \vec{e_\phi}}{\partial r}=0
$$
which is obvious because when $\theta$ and $\phi$ are fixed, the three vectors won’t change their directions.
$$
\frac{\partial \vec{e_r}}{\partial \theta}=\vec{e_\theta}
$$
$$
\frac{\partial\vec{e_\theta}}{\partial \theta}=-\vec{e_r}
$$
$$
\frac{\partial\vec{e_\phi}}{\partial \theta}=0
$$
Which is natural too, because the first two equation is the same as what we learnt earlier in the polar coordinate case. And the last one could be observed directly from the figure, unchanged.
$$
\frac{\partial \vec{e_r}}{\partial \phi}=\sin\theta \vec{e_\phi}
$$
$$
\frac{\partial\vec{e_\theta}}{\partial \phi}=\cos\theta\vec{e_\phi}
$$
$$
\frac{\partial\vec{e_\phi}}{\partial \phi}=-\sin\theta\vec{e_r}-\cos\theta\vec{e_\theta}
$$
The first equation could be verified by drawing the infinitesimal displacement angle. The above $\vec{e_r}$ shift angle $\Delta\alpha$, which satisfy $r\Delta\alpha=r\sin\theta\Delta\phi$ , i.e. $\Delta \alpha=\sin\theta\Delta\phi$:
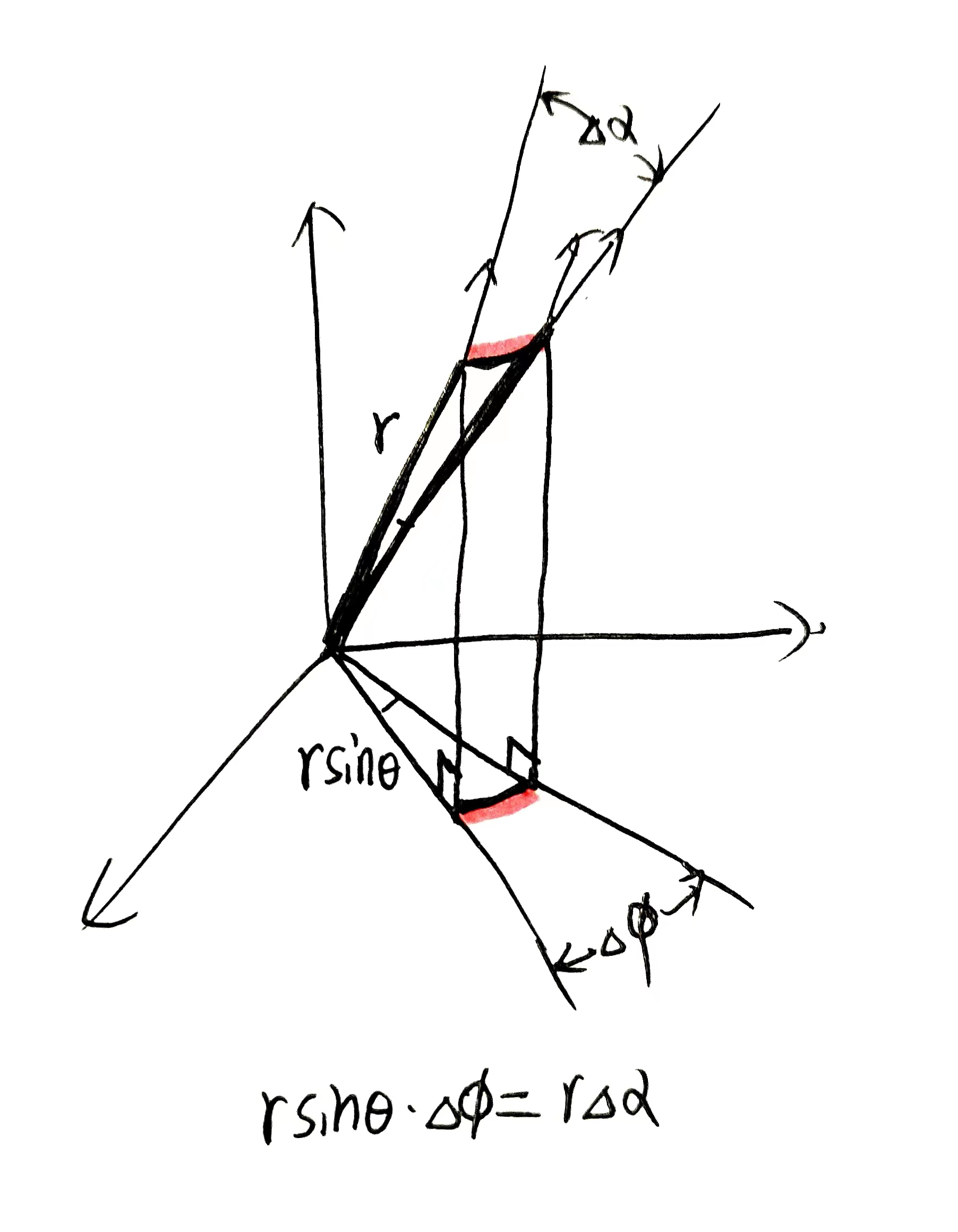 for the second equation, much the same:
for the second equation, much the same:
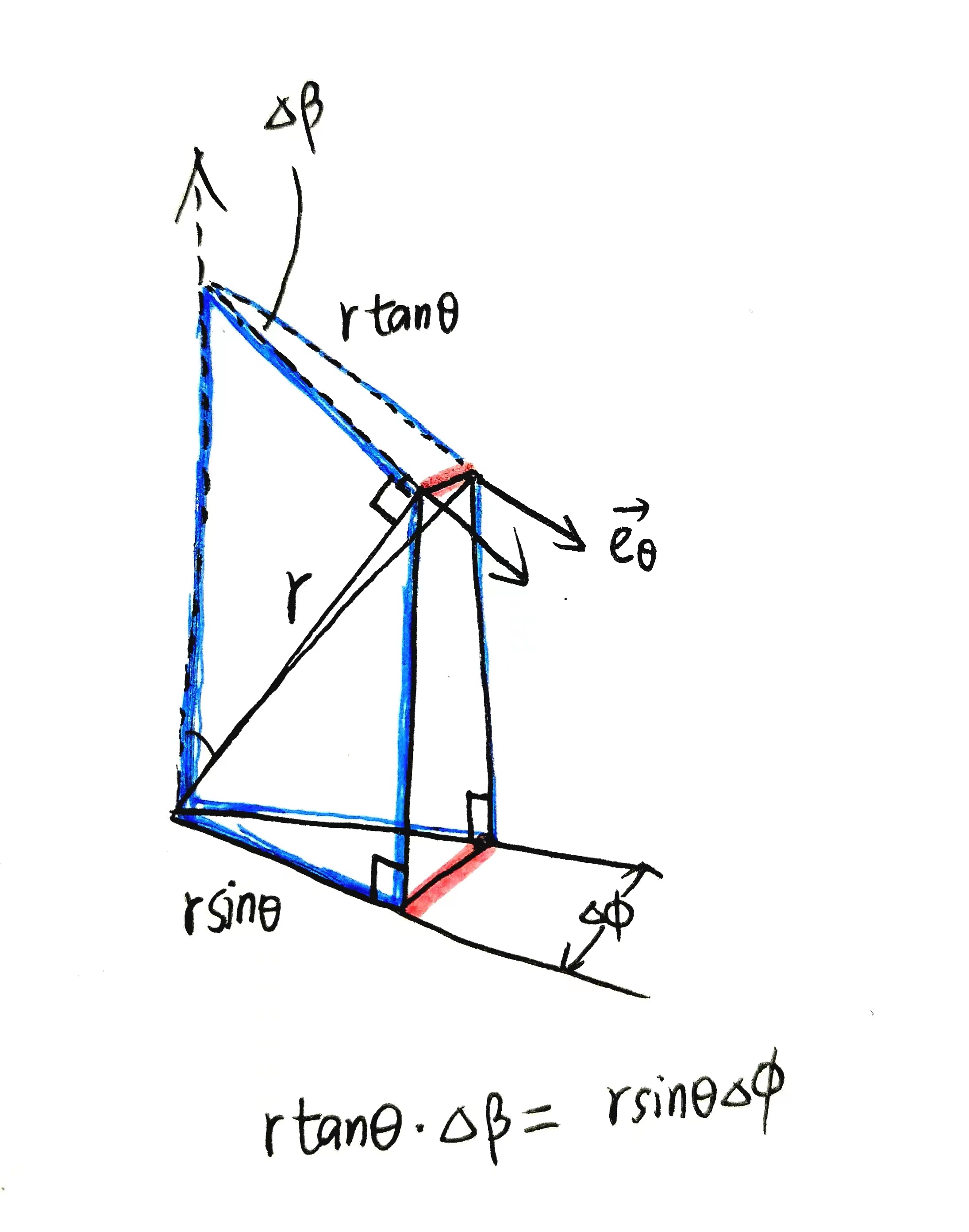
as for $\vec{e_\phi}$, $\Delta\vec{e_\phi}$ points inward to the origin (similar to polar coordinate case), thus the direction is a linear combination of $\vec{e_r}$ and $\vec{e_\phi}$:
$$
\sin\theta\vec{e_r}+\cos\theta\vec{e_\theta}
$$
thus the Laplacian:
$$
\begin{align*}
\nabla\cdot\nabla
&=\nabla\cdot\left(\vec{e_r}\frac{\partial u}{\partial r}+\vec{e_\theta}\frac{1}{r}\frac{\partial u}{\partial \theta}+\vec{e_\phi}\frac{1}{r\sin \theta}\frac{\partial u}{\partial \phi}\right)
\newline
\newline
&=\left([\vec{e_r}\frac{\partial }{\partial r}]+[\vec{e_\theta}\frac{1}{r}\frac{\partial }{\partial \theta}]+[\vec{e_\phi}\frac{1}{r\sin \theta}\frac{\partial }{\partial \phi}]\right)
\left(\vec{e_r}\frac{\partial u}{\partial r}+\vec{e_\theta}\frac{1}{r}\frac{\partial u}{\partial \theta}+\vec{e_\phi}\frac{1}{r\sin \theta}\frac{\partial u}{\partial \phi}\right)
\newline
\newline
&=[\frac{\partial^2 u}{\partial r^2}]+[\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}]
+[\frac{1}{r\sin\theta}(\sin\theta\frac{\partial u}{\partial r}+\cos\theta\frac{1}{r}\frac{\partial u}{\partial\theta}+\frac{1}{r\sin\theta}\frac{\partial^2 u}{\partial \phi^2})]
\end{align*}
$$
where three $[\dots]$ linked the corresponding terms to three dot products in divergence.
$\square$
The pdf version of Mathematical_Physics series:




